Computer Vision Algorithm

[TOC]

Point set registration

1.1Rigid registration

刚性注册：给定两个点集，刚性配准产生一个刚性变换，该变换将一个点集映射到另一个点集。刚性变换定义为不改变任何两点之间距离的变换。通常，这种转换包括平移和旋转。[12]在极少数情况下，点集也可能会被镜像。在机器人技术和计算机视觉中，刚性配准应用最多。

1.2Non-rigid registration

给定两个点集，非刚性配准产生一个非刚性转换，该转换将一个点集映射到另一个点集。非刚性变换包括affine仿射变换，例如缩放和剪切贴图。但是，在点集配准的情况下，非刚性配准通常涉及非线性变换。如果已知点集变化的本征模式，则可以通过特征值对非线性变换进行参数化。[13]非线性变换也可以参数化为(TPS)薄板样条。[14] [13]

Registration algorithm

三维点集拟合

PPF –2010

算法的精髓：“整体建模，局部匹配”

【6D位姿估计】Point Pair Feature (PPF)

(学习opencv)Surface Matching之PPF Point Pair Feature 点对特征

Others

机器视觉之 ICP算法和RANSAC算法

三维点集拟合：平面拟合、RANSAC、ICP算法

平面拟合

SVD ：
- 根据协方差矩阵的SVD变换，最小奇异值对应的奇异向量就是平面的方向。
- 注意：这个方法是直接的计算方法，没办法解决数值计算遇到的病态矩阵问题.在公式转化代码之前必须对空间点坐标进行近似归一化！
使用法线方法
- 使用合适的方法剔除离群点，计算点云的形心P；
- 若在已经获得法线的点云中，可以对法线进行剔除离散点之后，求取最小方差的均值，直接求得法线方向N( alpha, beta, theta )；
- 使用点法式描述三维平面；或者根据形心P和法线方向，计算出平面方程的一般式。
空间向量的旋转

Ransac 1981

“RANdom SAmple Consensus（随机抽样一致）”

[ICP-ptp] Point-to-Point –1992

点云匹配：ICP（Iterative Closest Point迭代最近点）

ICP_SVD

matlab: https://github.com/ToughStoneX/3D_ICP

open3d-python: http://www.open3d.org/docs/release/tutorial/Basic/icp_registration.html

[ICP-ptl] Point-to-Plane ICP –2001

Efficient variants of the ICP algorithm. In 3-D Digital Imaging and Modeling, 2001.

Rusinkiewicz和M.Levoy。ICP算法的高效变体。在3D数字成像和建模中，2001年

GMMREG 2010

《A Robust Algorithm for Point Set Registration Using Mixture of Gaussians 2005》 Bing Jian

《Robust Point Set Registration Using Gaussian Mixture Models 2010》Bing Jian

Colored Point Cloud Registration 2017

Colored Point Cloud Registration Revisited, ICCV, 2017. J.Park, Q.-Y. Zhou, and V. Koltun

该算法比以前的点云配准算法更准确，更健壮，而运行速度与ICP配准的运行速度相当。

Global Registration

ICP和彩色点云登记被称为当地的，因为它们依赖于一个粗略的排列为初始登记的方法。本教程介绍了另一类注册方法，称为全局注册。该算法系列不需要对齐即可进行初始化。它们通常产生不太严格的对齐结果，并用作局部方法的初始化。

Fast global registration –2016

RANSAC 《Fast Global Registration, ECCV》, 2016. Q.-Y. Zhou, J. Park, and V. Koltun

基于RANSAC的Fast global registration解决方案可能需要很长时间，这是因为有无数的模型建议和评估。 [Zhou2016]引入了一种更快的方法，该方法可以快速优化几乎没有对应关系的行处理权重。由于每次迭代都没有模型建议和评估，[Zhou2016]中提出的方法可以节省大量的计算时间。

该脚本比较了基于RANSAC的全局注册和[Zhou2016]的实现的运行时间。

Multiway registration

Robust Reconstruction of Indoor Scenes, CVPR, 2015. S.Choi, Q.-Y. Zhou, and V. Koltun

Multiway registration is the process to align multiple pieces of geometry in a global space. Typically, the input is a set of geometries (e.g., point clouds or RGBD images) $ {𝐏_𝑖} $. The output is a set of rigid transformations ${𝐓_𝑖}$, so that the transformed point clouds ${𝐓_𝑖 P_i} $ are aligned in the global space.

Supply

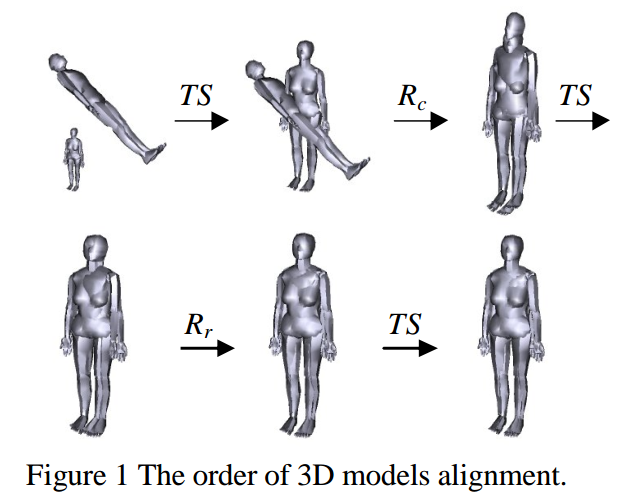
《Alignment of 3D models》

《A 3D Model Alignment and Retrieval System》

$TS -> R_c -> TS -> R_r -> TS$

AlignNet-3D

引言
Align(register) point clouds 即对齐(配准)点云，意思是将一个点云匹配到另一个点云上面，主要用来将从一个物体的不同角度得到的局部点云拼接起来，由此得到一个完整的3D模型，对点云做Alignment或Registration从本意上来说并没有什么本质的区别，尤其是在阅读学术论文的时候。

但是我在工作中所了解到的是Alignment是把几个3D相机固定起来，然后计算出这几台3D相机点云之间相对位置的转换矩阵，一般情况下以第一个相机的坐标系为基准，把其他相机的点云通过转换与平移移到相同的坐标系下，然后可以实时捕捉完整的3D点云。而Registration则指的是只用一台3D相机，连续从各个角度对一个物体进行扫描，然后把把得到的点云一帧一帧的拼接起来，由此而得到完整的3D模型。所以从这个角度来说，Alignment得到完整模型是实时的，是多个相机同一时间从多个角度得到的点云拼接起来，每一帧都是完整模型，Registration则是一台相机从不同时间不同角度的到点云拼接，完整3D模型不是实时的，需要通过离线处理得到。但其本质均是通过得到点云之间的转换矩阵来实现匹配。

常见的Alignment或Registration算法
最常见的Alignment算法即ICP(Iterative Closest Point)及其各种变体,如其名字所示，此方法是通过先对点云进行初配准，然后迭代最近点使相对应的点距离最小而得到一个转换矩阵。以下对Point-to-point ICP和Point-to-plane ICP这两种ICP方法做简要介绍：

Point-to-point & Point-to-plane ICP

一般来说，此ICP算法会迭代两个步骤：

（1）找到目标点云P和源点云Q中相对应的点集K={(p,q)}，定义p与q的目标函数E(T)和q到p的转换矩阵T,不同的ICP变体使用不同的目标函数E(T)。
（2）通过最小化目标函数E(T)来更新变换T。
point-to-point ICP使用的目标函数如下所示

而point-to-plane ICP使用了一个不同的目标函数

AlignNet-3D介绍
AlignNet-3D是论文AlignNet-3D: Fast Point Cloud Registration of Partially Observed Objects里研究的一种align点云的方法，论文主要研究了智能汽车的精确3D跟踪状态估计，提出了一个以学习为基础的方法AlignNet-3D来对不同时间捕获的汽车点云做Alignment，以此来估计汽车近距离内的精确运动，作者的评估表明AlignNet-3D在计算上优于global 3D registration，同时显著提高了效率。

论文创新点，参考论文所使用的方法都是直接通过优化计算转换的算法，而此论文是通过学习的方式来Align点云，因此，它可以受益于额外的训练数据，并对遮挡和截断具有鲁棒性。

方法简述，论文的方法可以概述为给定一个物体在不同时间捕获的两个点云，然后通过对观测到的点云做Alignment来精确地估计物体的相对运动，如下图所示：
————————————————
版权声明：本文为CSDN博主「Asher_zheng」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/Asher_zheng/article/details/103094927

Aligning 3D Data

动机：

形状检查
运动估计
外观分析（我们所做的）
纹理映射 (Texture mapping) 一般应用于2D到3D的UV Map
跟踪

How to find correspondences: User input? Feature detection? Signatures?（用户输入？特征检测？签名？）

Alternative(备选方案): assume closest points correspond 假设最接近的点

计算机视觉--点云对齐