[TOC]

A Survey of Rigid 3D Pointcloud Registration Algorithms 2014

Principal Component Analysis(PCA)

Singular Value Decomposition (SVD),

Iterative Closest Point (ICP)

刚性3D点云配准算法研究 2014

使用深度传感器（例如飞行时间相机）获得的3D点云的几何对齐对于机器人技术和计算机视觉中的重要应用而言是一项艰巨的任务。由于便宜的深度感测设备的最新出现，文献中提出了许多不同的3D配准算法，着重于不同的领域，例如定位和映射或图像配准。在这篇调查论文中，我们回顾了最新的注册算法，并讨论了它们的通用数学基础。从简单的确定性方法（例如主成分分析（PCA）和奇异值分解（SVD））开始，对最近引入的方法（例如迭代最近点（ICP）及其变体）进行了分析和比较。

从简单的确定性方法（例如主成分分析（PCA）和奇异值分解（SVD））开始，对最近引入的方法（例如迭代最近点（ICP）及其变体）

阅读笔记（CVPR2015）Non-Rigid Registration of Images With Geometric and Photometric Deformation……

https://blog.csdn.net/miracle0_0/article/details/82839534

傅里叶矩匹配（FMM）的加权重叠局部仿射图像配准算法[22]

Smooth Shells: Multi-Scale Shape Registration with Functional Maps

https://github.com/marvin-eisenberger/smooth-shells

https://arxiv.org/abs/1905.12512

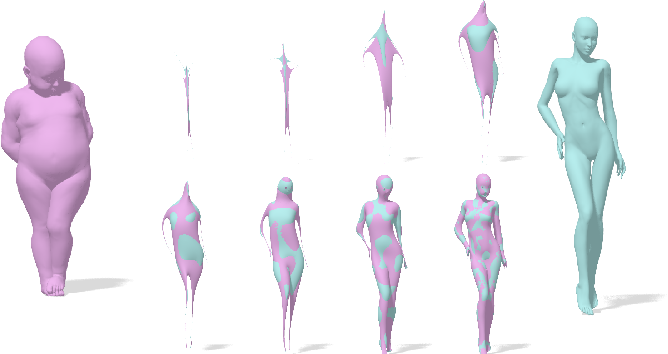
Numerical Geometry of Non-Rigid Shapes

2009 book

从微观到宏观，可变形物体在我们周围的世界中无处不在。从医学到安全性的广泛应用都需要研究这种形状并对其行为进行建模。近年来，非刚性形状吸引了越来越多的兴趣，这导致了该领域的快速发展，其中最先进的技术源于截然不同的科学领域-理论和数值几何，优化，线性代数，图论，机器学习和计算机图形学（仅举几例）被用于寻找解决方案。

Functional maps: a flexible representation of maps between shapes

2012

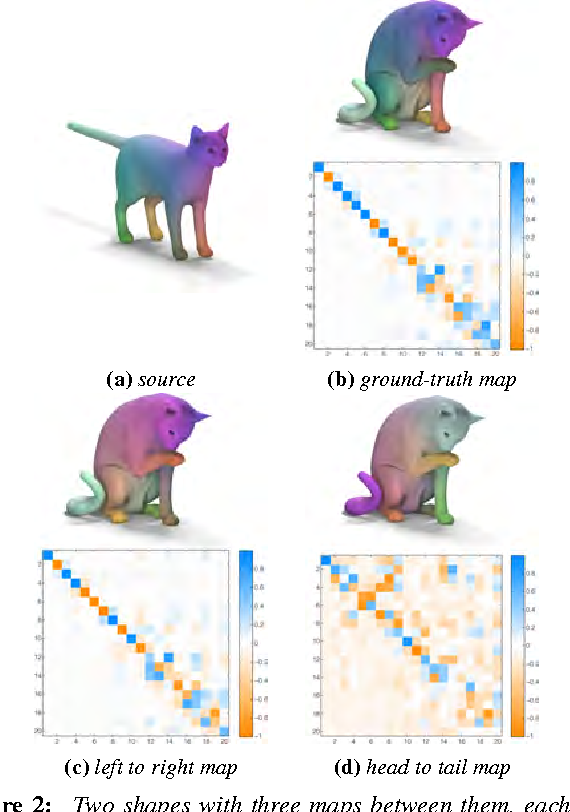
Figure 2: Two shapes with three maps between them, each rendered as a point-to-point mapping through color correspondence (top) and its functional representation (bottom) with colors proportional to matrix values. Note that the least isometric map in (d) leads to a less sparse functional matrix.

Shape Analysis via Functional Map Construction and Bases Pursuit

2019

Fig. 1. Given a pair of shapes and a collection of corresponding descriptors, our method produces a set of basis elements along with an associated functional map. These bases are not necessarily LB smooth and thus their aligning matrix is typically dense (left). Our machinery can be utilized in various geometry processing tasks such as non-isometric shape matching (right).

Eigen-System

https://www.sciencedirect.com/topics/mathematics/eigensystem

数值分析手册，2019 5.3 Laplace–Beltrami特征图方法

5.3 使用LB特征图进行非刚性歧管配准

拉普拉斯-贝尔特拉米算子（Laplace–Beltrami operator）

Riemann Surface 黎曼曲面