无人驾驶（10）路径规划

Posted on | In , |

  • 什么是规划

    • 规划的本质
    • 如何解决一个规划问题

  • 传统的规划方法

    • 机器人学基础
    • 经典算法

  • 无人车规划

    • Routing
    • Planning
    • Lattice Palnner

  • Apollo 如何求解规划问题

    • EM Planner
    • DP， QP求解

[toc]

What is motion planning?

  • planning
  • 本质是什么

$$
argmin_xf(x)
$$

  • 搜索问题
    • Google: Quary词，返回给最优结果。
    • 无人车：当前环境和当前状态，当前库路径上最优选择。
    • 什么是好规划？
  • “好”其实就是个目标函数：f(x)
    • f(x)的最优解

Motion Planning 的三个领域

  • Robotics Fileds:(机器人领域)
    • 生成轨迹实现目标
    • 常用方法： RRT，A*, D*, D*lite
  • Control Theory:(控制领域)
    • 方式：动态系统理论实现目标状态
    • 方法：MPC , LQR
  • AI：生成状态和Action的映射

如何解决一个Motion Panning 问题？

  • 找一个简单的突破口
    • 将问题转换成一个简单的问题：Path Finding Problem
      • 不关心速度，不关心走
      • 周围固定
  • 简言之就是，路径选择问题
    • A sample shortest path example
    • 什么样的path是最好的？这是重点
      • 路径最短
        • BFS，DFS
        • Dijkstra
    • 刚刚看到的Search属于non-information search 效率较低
    • A* search: 基于Dijkstra的改进算法【基础算法，很重要】
    • 无人机中的规划和A* search相差多远？
      • 部分感知
      • 动态障碍物
      • 复杂环境: 交通规则，碰瓷
      • A*本身是一个Global Algorithm
        • Global Routing

Partial Observed situation

  • 贪心算法

    • incremental search增量搜索：目前状态求解道最优

  • p* star

    • 部分环境信息的一个Search
    • Apollo登月小车
    • 改进版：D* lite

  • 可以求解全局最优？

    • 有难度

    • 一定必要全局最优吗？

      • Stentz Anthony，“Optimal and Efficient Path Planing for Partially-Known Enviroments”, 1994

        • （统计学教授）通过部分最优，可以逼近全局最优

  • Informative & Non-informative Search

    • Global & Partial observed

  • 至此，我们已经有了如下几个方法：

    • 目标函数并且结合了平滑性和目标Cost
    • 使用通用的Search方法来最小化Cost从而找到一个最优解
    • 通过Partial observed information来做局部planning

  • 我们还缺什么？

    • 处理动态障碍物，动态环境
    • 处理交通规则
    • 实时计算
      • （100ms-150ms）
      • 人一般反应时间300-500ms
      • 有效时间内找到最优解
      • c++

  • 给无人车motion planning下一个定义：

    • Safely

    • Smoothly

    • Achieve to destination

    • X, Y, Time: 3D trajectory optimization problem

    • 无人车硬件系统

      • 定位
      • 感知

    • 无人车软件信息

      • 动态信息
      • 静态信息
        • HD Map
          • 实时性保证

    • 如何设计出一个合理轨迹？

      • 路径Path
      • 速度Speed

经典参考书籍

  • Steve Lavelle, Motion Planning Algorithms

  • Principles of Robot Motion: Theory, Algorithms and implementations

经典文献

  • A Review of Motion Planning for automated Vehivles

基本Planning方法

  • 经典基于环境建模的方法

    • RRT
    • Lattice

  • 现代无人车Planning方法

    • Darpa

    • Lattice in Frenet Frame

    • Spiral polymial

      A Review of Motion Planning Techniques for Automated Vehicles

  • 质点模型

    • 物体看车一个质点
    • 点与点不相碰

  • 刚体问题

    • BycicleModel
    • XY Heading
    • Collision

  • Planning限制条件

    • 避免膨胀
    • 边界阈值（跟车距离等）

  • 连续空间问题怎么解？

    • 离散化
    • 网格化

传统机器人基础

  • PRM （Probabilistic Roadmap Planning）

    • 非常常用三维一个方法
    • 连续空间离散化
      • 随机撒点
      • Obstacle上的点删除
    • 连续可行点，形成可行空间
    • A*

  • RRT（Incremental version of PRM）PRM的增量式的版本

    • 使用增加搜索的方式来进行
      • 找附近可行点的最优点
      • F(x) 最小，Cost最小
      • 走过车中也不能碰到障碍物
      • 撒点距离不能太远
        • 一步一步的移动

  • Lattice 方法

    • 改进了RRT的折线问题
    • 给出Path的平滑曲线
    • 网格化
      • 每个采样格中都是用曲线连接
    • 指数级别的一个搜索算法（NP-Hard)

  • DP（动态规划）

    • 减少搜索空间
      • 服用已有结果
    • Lattice DP的平滑度够吗？
      • 曲率连续
      • 曲率导数不一定连续【此是大问题，–方向盘突然就打大的角度变化】

  • QP（二次规划）

    • 凸优化问题最优化求解

    • 公式表达
      $$
      minimize \frac{1}{2} X^T QX+c^TX \
      subject: Ex = d , Fx \leqslant m
      $$

    • 性质：再凸优化中的图空间问题，用QP有最优解

    • QP如何找到平滑曲线

      • $ min|f’|^2$
      • $ min|f’’|^2$
      • $ min|f’’’|^2$

    • 其它的平滑曲线方法还有贝塞尔曲线，样条插值方法

  • 刚体模型

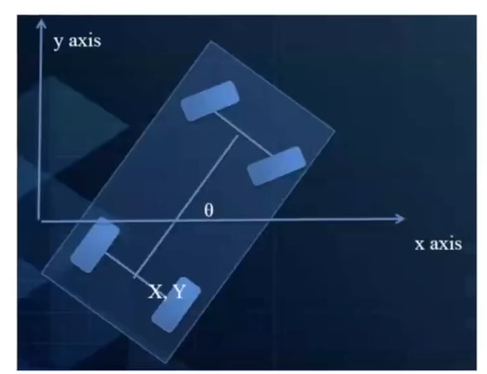
  • image-20220501021506769

    • 前轮转向和Heading的关系

      • 前轮是沿着切线的方向行驶
      • 前后轮是同一个旋转中心
      • 左右轮的结构相同

    • Bicycle Model

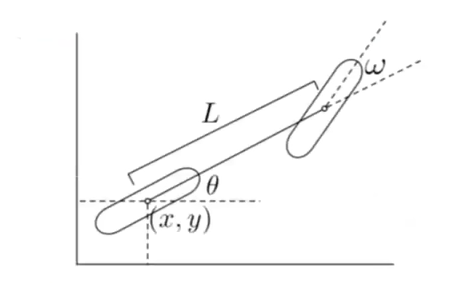
    • image-20220501021446166

      • 曲率公式
        $$
        \frac{1}{R} = kappa = (tan(\omega)) / L
        $$

无人车Planning

  • 定义

    从A点到B点，构建一个车辆运动归结，结合HD Map Localization 和Prediction

    • 输入
    • 输出：可行是归家，有一系列点组成
    • 两个层面，导航界面，运动轨迹层面

  • Routing

    • 导航一条A到B的全局路径
    • 输入：地图（路网信息，交通状态），当前位置，目的地（乘客定）
    • 输出：可行驶道路的连接线
    • 搜索：地图数据转化成图网络
      • 节点表示道路
      • 边代表道路连接

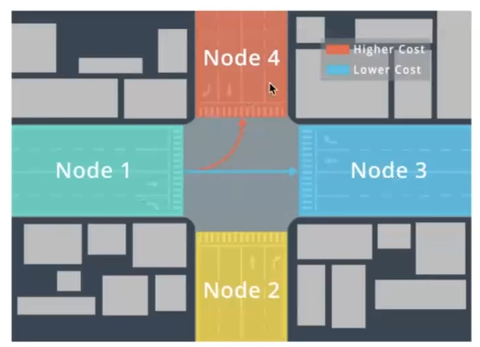
    image-20220501021924135

  • A*经典算法

    • 最经典的路径查找算法
    • F(n) = G(n) + H(n)