SLAM 三维刚体运动

Posted on | In , |

SLAM三维刚体运动（Eigen）

1、旋转矩阵

2、实践Eigen

1
2
3
4
5
6
7
8
Eigen::Matrix3d matrix_33 = Eigen::Matrix3d::Zero(); //初始化为零
matrix_33 = Eigen::Matrix3d::Random();
matrix_33.transpose();    // 转置
matrix_33.sum();    // 各元素和
matrix_33.trace();    // 迹
10* matrix_33; // 数乘
matrix_33.inverse();    // 逆矩阵
matrix_33.determinant(); // 行列式
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
 -0.997497   0.617481  -0.299417
  0.127171   0.170019   0.791925
 -0.613392 -0.0402539    0.64568
 transpose
 -0.997497   0.127171  -0.613392
  0.617481   0.170019 -0.0402539
 -0.299417   0.791925    0.64568
 sum
0.401715
 trace
-0.181799
 x
 -9.97497   6.17481  -2.99417
  1.27171   1.70019   7.91925
 -6.13392 -0.402539    6.4568
 inverse
-0.271556    0.7412  -1.03501
  1.08862   1.58676  -1.44134
-0.190108  0.803059  0.475647
 determinant
-0.521644

3、旋转向量和欧拉角

  • 欧拉角–人机交互，方便人的理解；

  • 计算时较少应用；

图片

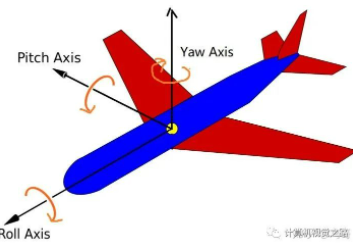
转换关系：

  • 旋转向量(轴角)–》旋转矩阵：罗德里格斯公式Rodriguez‘s Formula

$$
R = cos\theta I + (1-cos \theta )nn^T + sin\theta n^{\hat{}} \tag{3.14}
$$

“^” 是向量到反对称的转换符（见3.3）

  • 旋转矩阵-》旋转向量（轴角）

转角θ有：

$$
tr(R) = \cos\theta tr(I) + (1-\cos\theta)tr(nn^T) + \sin\theta tr(\hat{n}) \
= 3 \cos\theta + (1-\cos\theta ) \
= 1 + 2\cos(\theta)
\tag{3.15}
$$

因此

$$
\theta = arccos( \frac{tr(R)-1}{2}) \tag{3.16}
$$

转轴n：由于旋转轴上的向量在旋转后不发生改变，说明

$$
Rn=n
$$

因此，转轴n是矩阵R特征值1对应的特征向量；求解+归一化，就得到了旋转轴；

4、四元数

复数基础

知乎- 复数与旋转

# 四元数——基本概念(原理很详细)

《Visualizing Quaternions》，四元数可视化

大多数技术博客来说，写的已经非常全面详尽。但是对于复数和四元数的关联，四元数的指数对数运算，还有一些四元数的理解显然由于篇幅原因没有说的太清晰，个人觉得这部分参考上面推荐的书就行了，该文章最核心的部分在于对旋转的描述，通过实例，极为清晰地介绍了四元数怎么去旋转一个三维向量。下面给出文章的链接。

英文原版：Understanding Quaternions 中文翻译：理解四元数

《Quaternions For Computer Graphics》这本书对于四元数如何应用于旋转，从原理到实践都说的非常详细，正好弥补第一本书籍的不足。

四元数相比其他形式的优点：

  • 解决万向节死锁（Gimbal Lock）问题
  • 仅需存储4个浮点数，相比矩阵更加轻量
  • 四元数无论是求逆、串联等操作，相比矩阵更加高效

主流应用：缩放向量+旋转四元数+平移向量

复数：

$$
z=a+bi \
(a, b 是任意实数) \
i^2 = -1 \
|z| = \sqrt{a^2+b^2}
$$

所以，复数z的矩阵形式定义为：

$$
z =
\left[
\begin{matrix}
a & -b \
b & a
\end{matrix}
\right]
$$

复数代表的2D旋转

复平面，假设向量z与实轴夹角为$\theta$,则：

$$
\theta = atan2(b,a) \
cos(\theta) = a / \sqrt{a^2 + b^2 } \
sin(\theta) = b / \sqrt{a^2 + b^2 } \
$$

所以：

$$
z = a +bi =
\left[
\begin{matrix}
a & -b \
b & a
\end{matrix}
\right]
= \sqrt{a^2 + b^2}

\left[
\begin{matrix}
a/\sqrt{a^2 + b^2} & -b/\sqrt{a^2 + b^2} \
b/\sqrt{a^2 + b^2} & a/\sqrt{a^2 + b^2}
\end{matrix}
\right] \
= \sqrt{a^2 + b^2}
\left[
\begin{matrix}
cos(\theta) & -sin(\theta) \
sin(\theta) & cos(\theta)
\end{matrix}
\right]
$$

其代表的是一个旋转+缩放变换:

1、逆时针旋转 $\theta$ 度

2、缩放$\sqrt{a^2 + b^2}$

四元数

$$
q = q_0 + q_1i + q_2j + q_3k \tag{3.17}
$$

三个虚部的关系：

$$
i^2 = j^2 = k^2 = -1 \
ij = k, ji = -k \
jk = i, kj = -i \
ik = j, ki = -j \tag{3.18}
$$

标量+向量，表达四元数

$$
q = [s, v] , s = q_0 \in R, v = [q_1, q_2, q_3]^T \in \R^3
$$

假设旋转是绕单位向量$n=[n_x, n_y, n_z]^T$进行了角度θ的旋转，那么四元数形式为：

角轴–》四元数

$$
q = [ cos\frac{\theta}{2}, n_x sin\frac{\theta}{2},
n_y sin\frac{\theta}{2}, n_z sin\frac{\theta}{2}, ]^T \tag{3.19}
$$

四元数-》角轴

$$
\theta = 2arccos(q_0) \

[n_x, n_y, n_z]^T = \frac{[q1, q2, q3]^T}{\sin( \frac{\theta}{2})}

\tag{3.20}
$$

运算

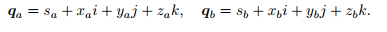
加减

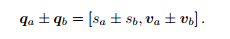
乘法

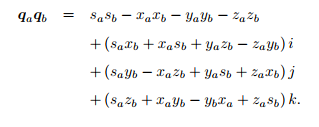
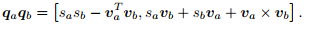
共轭 $ q^*_a = s_a - x_ai - y_aj - z_ak = [s_a, -v_a]$

模长 $ ||q_a||= \sqrt{s_a^2 + x_a^2 + y_a^2 + z_a^2 } $

逆 $ q^{-1} = q^* / || q||^2$

数乘 $ kq = [ks, kv]$

点乘 $q_a \sdot q_b = s_a s_b + x_a x_b i+ y_a y_b j + z_a z_b k $

四元数表示旋转

三维空间点，用一个虚四元数表示

$$
p = [0, x, y, z ] = [0, v]
$$

四元数q表示旋转(参照3.19)

$$
q = [\cos(\frac{\theta}{2} ), n \sin(\frac{\theta}{2})]
$$

旋转后：

$$
p^{‘} = q p q^{-1}
$$

四元数与角轴的关系

5、*相似、仿射、射影变换

6、Eigen几何模块

7、可视化

  • 世界坐标系（一旦确定，就永远固定）

  • 相机坐标系

设某点在世界坐标系中坐标为$p_w$ ,在相机坐标系下为 $p_c$那么：

$$
p_c = T_{cw}p_w
\
p_w = T_{cw}^{-1}p_c \tag{3.40, 3.41}
$$

$p_c$ 取零向量，也就是相机坐标系的原点，那么，此时$p_w$就是相机原点在世界坐标系下的坐标：

$$
p_w = T_{wc}0 = t_{wc} \tag{3.42}
$$

这个正是T_wc的平移部分，因此可以从T_wc中直接看到相机在何处，这也是我们说T_wc更为直观的原因。

8、总结

1、

2、验证3.34（四元数旋转某个点后，结果是一个虚四元数，所以仍然对应一个三维空间点）

3、总结转换关系

图片
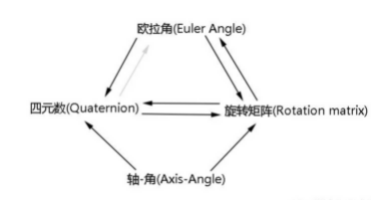
—> 旋转矩阵 轴角 欧拉角 四元数
旋转矩阵 - 3.15
轴角 3.14 - \ 3.19
欧拉角 \ -
四元数 3.20 -

那么下文我们都采用ZXY顺规来推导公式！采用列主向量(column major)！(但是注意DirectXMath API生成的矩阵其实是行主向量(row major)的)

欧拉角–》旋转矩阵

$$
\begin{aligned}
R(\alpha, \beta, \gamma) &= R_y(\alpha)R_x(\alpha)R_z(\alpha) \
&= \left[\begin{matrix} cos\alpha & 0 & sin\alpha \ 0 & 1 & 0 \ -sin\alpha & 0 & cos\alpha \end{matrix} \right]
\left[\begin{matrix} 1 & 0 & 0 \ 0 & cos\beta & -sin\beta \ 0 & sin\beta & cos\beta \ \end{matrix}\right]
\left[\begin{matrix} cos\gamma & -sin\gamma & 0 \ sin\gamma & cos\gamma & 0 \ 0 & 0 & 1 \ \end{matrix}\right]
\
&= \left[\begin{matrix} c_1 & 0 & s_1 \ 0 & 1 & 0 \ -s_1 & 0 & c_1 \ \end{matrix}\right]
\left[\begin{matrix} 1 & 0 & 0 \ 0 & c_2 & -s_2 \ 0 & s_2 & c_2 \ \end{matrix}\right]
\left[\begin{matrix} c_3 & -s_3 & 0 \ s_3 & c_3 & 0\ 0 & 0 & 1 \ \end{matrix}\right]
\
&= \left[\begin{matrix} c_1 & s_1 s_2& s_1 c_2 \ 0 & c_2 & -s_2 \ -s_1 & c_1s_2 & c_1c_2\ \end{matrix}\right]
\left[\begin{matrix} c_3 & -s_3 & 0 \ s_3 & c_3 & 0\ 0 & 0 & 1 \end{matrix}\right]
\
&= \left[\begin{matrix} c_1 c_3 + s_1 s_2 s_3 & c_3s_1s_2 - c_1s_3& c_2s_1 \ c_2s_3 & c_2c_3& -s_2 \ 1 & s_1 s_3+c_1 c_3 s_2 & c_1 c_2 \ \end{matrix}\right]

\end{aligned}
\tag{100}
$$

其中：

$$
c1 = cos(\alpha)=cos(Y_{yaw}), s1 = sin\alpha = sin(Y_{yaw}) \
c2 = cos(\beta)=cos(X_{pitch}), s2 = sin\beta= sin(X_{pitch}) \
c3 = cos(\gamma)=cos(Z_{roll}), s3 = sin\gamma= sin(Z_{roll})
\tag{101}
$$

旋转矩阵–》欧拉角

(小白学视觉) 一文详解四元数、欧拉角、旋转矩阵、轴角如何相互转换