基础
微分PI也很困难,除非我们能把它转换成对数。求偏导

那么这个log的偏导怎么求呢?

回顾
- TD 和SARSA几乎一样,只是把V换成Q
$$
SARSA: Q(S,A) \larr Q(S,A) + \alpha[ R+ \gamma Q(S’,A’) - Q(S,A)] \
TD(0): V(S_t) \larr V(S_t) + \alpha[ R+ \gamma V(S_{t+1}) - V(S_t)] \
$$
Q-learning
- Qlearning公式和SARSA相比,就差那么一个max。
$$
QLeaning: Q(S,A) \larr Q(S,A) + \alpha[ R+ \gamma \max Q(S’, a) - Q(S,A)] \
$$
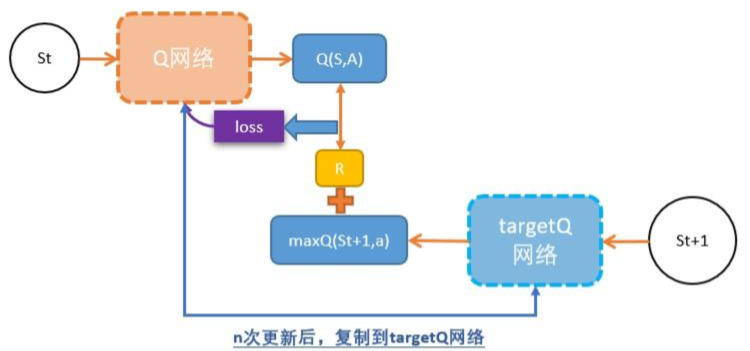
DQN
DQN = TD + 神经网络
DQN的深度网络,就像用一张布去覆盖Qlearning中的Qtable
DQN用magic函数,也就是神经网络解决了Qlearning不能解决的连续状态空间问题。
$$
Q(S,A) \larr Q(S,A )+ \alpha \big[
R + \gamma \max Q(S’, a) - Q(S,A)
\big]
$$
DoubeDQN
- 新增一个TargetQ网络,解决DQN的Q网络的学习效率比较低,而且不稳定。
DuelingDQN
A + S = Q : S值与A值的和,就是原来的Q值。
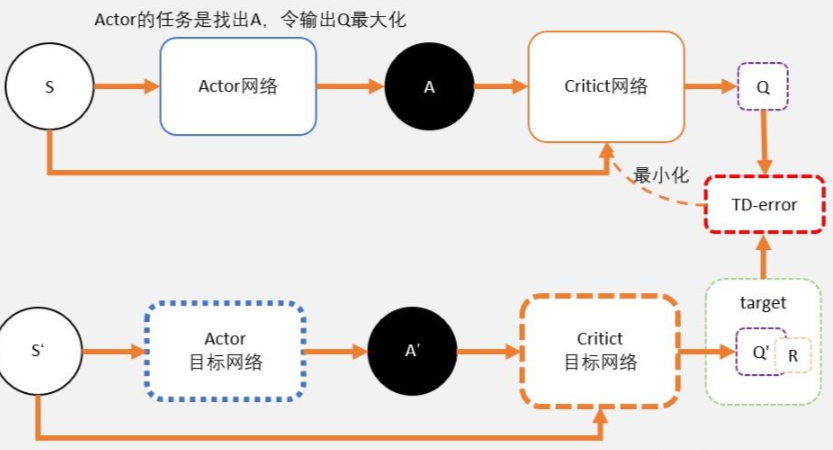
DDPG
DDPG就是用magic解决DQN不能解决的连续控制型问题。
也就是说,用一个magic函数,直接替代maxQ(s’,a’)的功能。也就是说,我们期待我们输入状态s,magic函数返回我们动作action的取值,这个取值能够让q值最大。这个就是DDPG中的Actor的功能。
我们之前讲DQN也说过,DQN的深度网络,就像用一张布去覆盖Qlearning中的Qtable。这也是DDPG中Critic的功能。
DDPG其实并不是PG,并没有做带权重的梯度更新。而是在梯度上升,在寻找最大值。
Critic
Critic网络的作用是预估Q,虽然它还叫Critic,但和AC中的Critic不一样,这里预估的是Q不是V;
注意Critic的输入有两个:动作和状态,需要一起输入到Critic中;
Critic网络的loss其还是和AC一样,用的是TD-error。
Actor
和AC不同,Actor输出的是一个动作;
Actor的功能是,输出一个动作A,这个动作A输入到Crititc后,能够获得最大的Q值。
所以Actor的更新方式和AC不同,不是用带权重梯度更新,而是用梯度上升。
常见算法公式
1、策略梯度法: $ \sum {t’=t}^{T} r(s{i,t’}, a_{i,t’}) - b_i$
2、状态值函数估计轨迹的return: $q(s,a)$
3、优势函数估计轨迹的return:$A(s,a) = q(s,a) - V(s,a)$
4、TD-Error 估计轨迹的return: $r(s,a) + q(s) - q(s’)$
Monte Carlo:
$V^{\pi}(s_t) = \sum^T_{t’=t} r(s_{t’}, a_{t’} )$
training data: ${s_{i,t}, V^{\pi}(s_t) }$
Loss: $ L = 1/2 \sum_i || \hat{V}^{\pi}(s_i) - y_i || ^2$
$$
V(S_t) \larr V(S_t) + \alpha [G_t - V(S_t)]
$$
蒙地卡罗需要完成整个游戏过程,直到最终状态,才能通过回溯计算G值。这使得PG方法的效率被限制。
那我们可不可以更快呢?相信大家已经想到了,那就是改为TD。
但改为TD还有一个问题需要解决,就是:在PG,我们需要计算G值;那么在TD中,我们应该怎样估算每一步的Q值呢?(答案是神经网络)
TD(bootstrap):
training data: $ { s_{i,t}, r(s_{i,t}, a_{i,t} ) + \hat{V}^{\pi}{\phi}( s{i, t+1}) }$
引入bias,–> 减少方差variance
AC: ac-zhihu
Actor: 一个输出策略,负责选择动作;
Critic: 一个负责计算每个动作的分数。
$$
\nabla L_{\theta} = \frac{1}{N} \sum_{i=1}^{N} \sum_{t=0}^{T} \Big[ \nabla_{\theta} log \pi_{\theta}(a_{i,t}|s_{i,t}) \Big(r(s_{i,t}, a_{i,t}) + \gamma \hat{V}{\phi}^{\pi} (s{i,t+1}) - \hat{V}{\phi}^{\pi}(s{i,t}) - b_i \Big) \Big]
$$
lower variance with bias
总结下TD-error的知识:
为了避免正数陷阱,我们希望Actor的更新权重有正有负。因此,我们把Q值减去他们的均值V。有:Q(s,a)-V(s)
为了避免需要预估V值和Q值,我们希望把Q和V统一;由于Q(s,a) = gamma * V(s’) + r - V(s)。所以我们得到TD-error公式: TD-error = gamma * V(s’) + r - V(s)
TD-error就是Actor更新策略时候,带权重更新中的权重值;
现在Critic不再需要预估Q,而是预估V。而根据马可洛夫链所学,我们知道TD-error就是Critic网络需要的loss,也就是说,Critic函数需要最小化TD-error。
Policy Gradient:
PG是一个蒙地卡罗+神经网络的算法。
策略评估
策略提升
VPG更新算法
$$
Policy Graditent: E_{\pi}[\nabla_{\theta}(log_{\pi}(s,a,\theta)) R(\tau)]
$$$$
Update rule: \Delta \theta = \alpha * \nabla_\theta (
log\pi(s,a,\theta)
) R(\tau)
$$$\pi : 策略函数,R(): score function 、alpha: lr $
$\nabla L_{\theta} = \frac{1}{N} \sum_{i=1}^{N} \sum_{t=0}^{T} \Big[ \nabla_{\theta} log \pi_{\theta}(a_{i,t}|s_{i,t}) \Big( \sum_{t’=t}^{T} \gamma^{t’-t} r(s_{i,t}, a_{i,t}) - b_i \Big)\Big]$
no bias with higher variance (because use single sample estimate)
PG算法,计算策略梯度的估计器,并将其插入随机梯度上升算法中。最常用的梯度估计器具有以下形式
$$
\hat{g} = \hat{E}t \Big[
\nabla{\theta} log {\pi}_{\theta}(a_t| s_t) \hat{A}_t
\Big] \tag{PPO-1}
$$
E: 表示有限批次样品的经验平均值。
Loss PG:
$$
L^{PG}(\theta) = \hat{E}t \Big[
log {\pi}{\theta} (a_t | s_t ) \hat{A}_t
\Big] \tag{PPO-2}
$$
结合AC + PG:
整条轨迹
$$
\nabla L_{\theta} =
\frac{1}{N} \sum_{i=1}^{N} \sum_{t=0}^{T}
\Big[
\nabla_{\theta} log \pi_{\theta}(a_{i,t}|s_{i,t})
\Big(
\sum_{t’=t}^{T} \gamma^{t’-t} r(s_{i,t}, a_{i,t})
- \hat{V}{\phi}^{\pi}(s{i,t})
\Big)
\Big]
$$
n-step:
$$
\nabla L_{\theta} =
\frac{1}{N} \sum_{i=1}^{N} \sum_{t=0}^{T}
[
\nabla_{\theta} log \pi_{\theta}(a_{i,t}|s_{i,t})
(
\sum_{t’=t}^{t+n} \gamma^{t’-t} r(s_{i,t}, a_{i,t})
- \hat{V}{\phi}^{\pi}(s{i,t})
)
]
$$
“vanilla” policy gradient / REINFORCE
TRPO
trust region / natural policy gradient methods
TRPO 与 PPO 之间的区别在于 TRPO 使用了 KL 散度作为约束条件,虽然损失函数是等价的,但是这种表示形式更难计算,所以较少使用。
约束下最大化更新:
$$
maxmize(\theta) \space \hat{E}t
\Big[
\frac{\pi{\theta}(a_t| s_t) }
{\pi_{\theta_{old}}(a_t | s_t)}
\hat{A}_t
\Big]
\tag{PPO-3,4}
$$
$$
subject \space to \space \hat{E}t
\Big[
KL \big[
\pi{\theta_{old}}(\cdot|s_t),
\pi_{\theta}(\cdot|s_t)
\big]
\Big] \leq \delta
$$
PPO思想1,使用panalty(惩罚)求解无约束优化问题
$$
maximize({\theta}) \space
\hat{E}t \Big[
\frac{\pi{\theta}(a_t| s_t) }
{\pi_{\theta_{old}}(a_t | s_t)}
\hat{A}t - \beta
KL\big[\pi{\theta_{old}} (\cdot| s_t),
\pi_{\theta} (\cdot| s_t)
\big]
\Big] \tag{PPO-5}
$$
相关算法
single path TRPO;
vine TRPO;
cross-entropy method (CEM)
covariance matrix adaption (CMA) 协方差矩阵自适应
natural gradient, the classic natural policy gradient algorithm
Max KL
RWR
PPO
CPI : conservative policy iteration 保守政策迭代 (普通的PG算法)
$$
L^{CPI}(\theta) = \hat{E}t \Big[
\frac{ \pi{\theta}(a_t| s_t) }
{\pi_{\theta_{old}}(a_t| s_t)}
\hat{A}_t
\Big]
= \hat{E}_t [
r_t(\theta) \hat{A}_t
] \tag{6}
$$
PPO_2-CLIP (PPO2思想,对ratio(分布比率)进行clip) 即取一个lower bound,保证梯度更新后效果不会变差
$$
L^{CLIP} (\theta)
= \hat{E}_t \Big[
min\Big(r_t(\theta) \hat{A}_t,
clip \big(r_t(\theta), 1-\epsilon, 1+\epsilon \big) \hat{A}_t \Big)
\Big] \tag{7}
$$
$\epsilon = 0.2$ , $L^{CLIP}$ 是$L^{CPI}$的下界。
PPO_1算法(Adaptive KL Penalty):
$$
L^{KLPEN} (\theta) = \hat{E}t \Big[
\frac{\pi{\theta}(a_t| s_t)}
{\pi_{\theta_{old}}(a_t| s_t)}
\hat{A}t - \beta
KL \big[
\pi{\theta_{old}} (\cdot| s_t),
\pi_{\theta} (\cdot| s_t)
\big]
\Big] \tag{8}
$$
$$
d = \hat{E}t \Big[
KL\big[
\pi{\theta_{old}} (\cdot| s_t),
\pi_{\theta} (\cdot| s_t)
\big]
\Big]
\
if d < d_{targ} / 1.5, \beta = \beta / 2 \
if d < d_{targ} \times 1.5, \beta = \beta \times 2
$$
PPO_2算法(完整目标函数)
$$
L_t^{CLIP+VF+S}(\theta) = \hat{E}_t
\Big[
L_t^{CLIP}(\theta)
- c_1 L_t^{VF}(\theta)
+ c_2 S\pi_{\theta}
\Big]
\tag{9}
$$
S: 表示entropy bonus,当actor和critic共享一套参数时,需要加的误差项 S :an entropy bonus,在exploration时很有用
$L_t^{VF}$ squared-error loss $(V_{\theta(S_t)} - V_t^{targ})^2$
PG Advantage Estimator:
$$
\hat{A}t = -V(s_t) + r_t + \gamma r{t+1} + …
+ \gamma^{T-t+1} r_{T-1}
+ \gamma^{T-t} V(s_T)
\tag{10}
$$
GAE也是用于平衡bias和variance的一种方法,公式比较复杂一点,思想是$TD(\lambda)$
truncated version of generalized advantage estimator(GAE):
$$
\hat{A}t = \delta_t + (\gamma \lambda )\delta{t+1} + … + … +
(\gamma \lambda )^{T-t+1 }\delta_{T-1} \tag{11,12} \
where \space \gamma_t = r_t + \lambda V(s_{t+1}) - V(s_t)
$$
No clipping or penalty:
$$
L_t(\theta) = r_t(\theta)\hat{A}_t
$$
Clipping:
$$
L_t(\theta) = min \Big(
r_t(\theta)\hat{A}_t,
clip\big(r_t(\theta), 1-\epsilon, 1+\epsilon\big)\hat{A}_t
\Big)
$$
KL penalty (fixed or adaptive)
$$
L_t(\theta) = r_t(\theta)\hat{A}t -
\beta KL
\big[
\pi{\theta_{old}}, \pi_{\theta}
\big]
$$