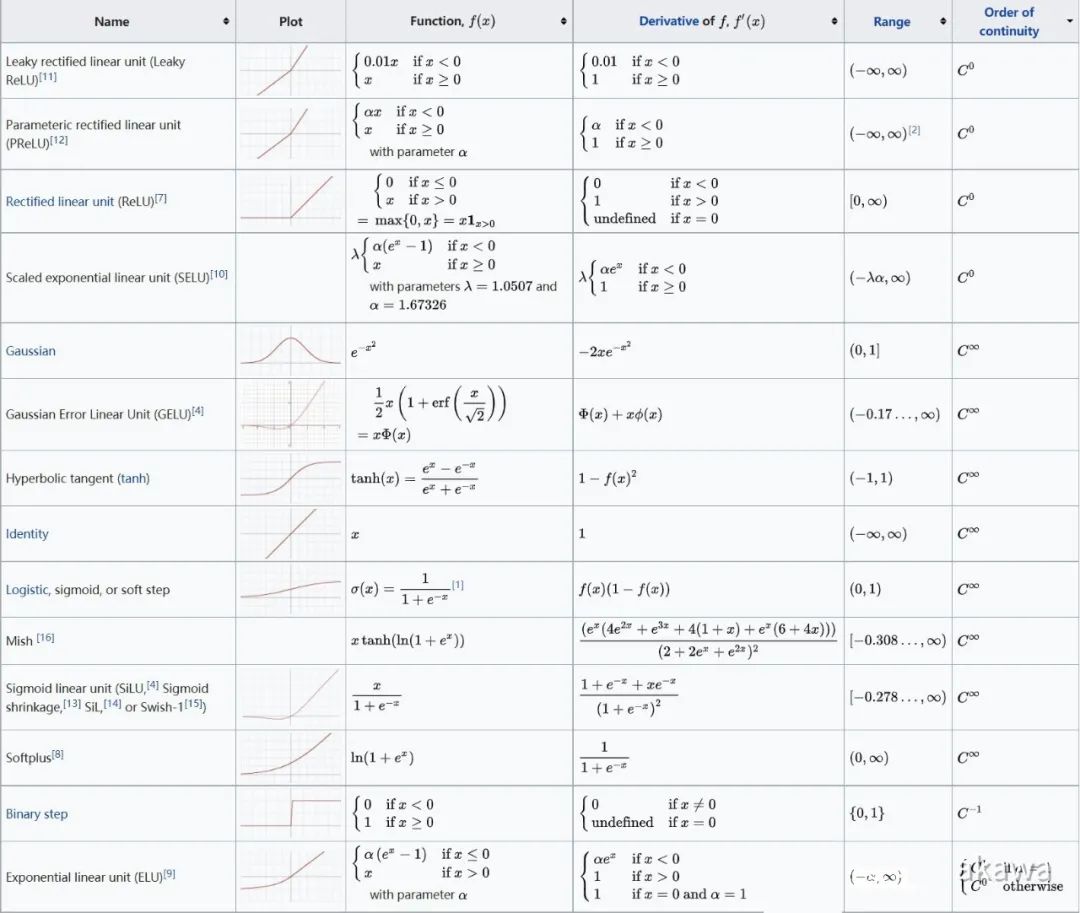
常见激活函数:
岭函数,径向函数,以及应用在卷积神经网络中的折叠激活函数。
| 岭函数 | 作用与输入变量的线性组合多元函数 | |
| 线性函数 | ||
| ReLU | ||
| Heaviside | ||
| Logistic | ||
| 径向激活函数 | 在欧几里得空间中求得点与点之间距离,作为通用的函数逼近器具有很好的效果。 | |
| 高斯函数 | ||
| 多项式函数 | ||
| 折叠激活函数 | 卷积神经网络中和多分类网络的输出层中 | |
| software | ||
常见激活函数
折叠函数
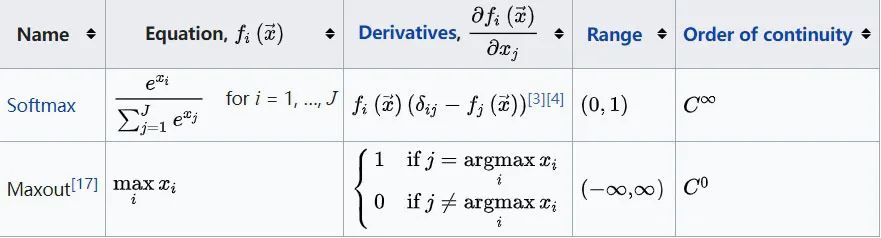
LangChain 就是一个 LLM 编程框架,你想开发一个基于 LLM 应用,需要什么组件它都有,直接使用就行;甚至针对常规的应用流程,它利用链(LangChain中Chain的由来)这个概念已经内置标准化方案了。下面我们从新兴的大语言模型(LLM)技术栈的角度来看看为何它的理念这么受欢迎。
借助 Langchain,可以创建聊天机器人、问答系统和其他人工智能代理。
其官方的定义
LangChain是一个基于语言模型开发应用程序的框架。它可以实现以下应用程序:
LangChain的主要价值在于:
现成的链使得入门变得容易。对于更复杂的应用程序和微妙的用例,组件化使得定制现有链或构建新链变得更容易。

大语言模型技术栈由四个主要部分组成:

微分PI也很困难,除非我们能把它转换成对数。求偏导

那么这个log的偏导怎么求呢?

$$
SARSA: Q(S,A) \larr Q(S,A) + \alpha[ R+ \gamma Q(S’,A’) - Q(S,A)] \
TD(0): V(S_t) \larr V(S_t) + \alpha[ R+ \gamma V(S_{t+1}) - V(S_t)] \
$$
$$
QLeaning: Q(S,A) \larr Q(S,A) + \alpha[ R+ \gamma \max Q(S’, a) - Q(S,A)] \
$$
DQN = TD + 神经网络
DQN的深度网络,就像用一张布去覆盖Qlearning中的Qtable
DQN用magic函数,也就是神经网络解决了Qlearning不能解决的连续状态空间问题。
$$
Q(S,A) \larr Q(S,A )+ \alpha \big[
R + \gamma \max Q(S’, a) - Q(S,A)
\big]
$$
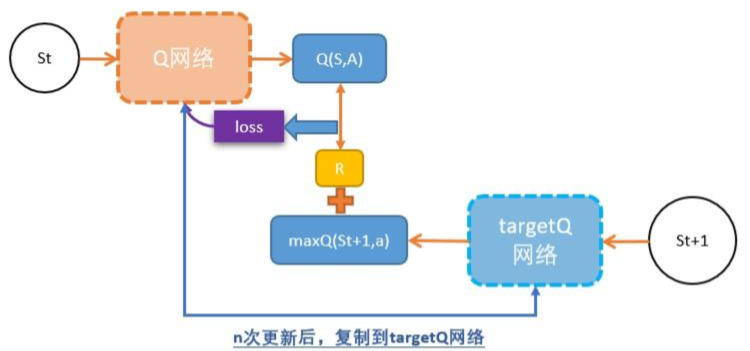
A + S = Q : S值与A值的和,就是原来的Q值。
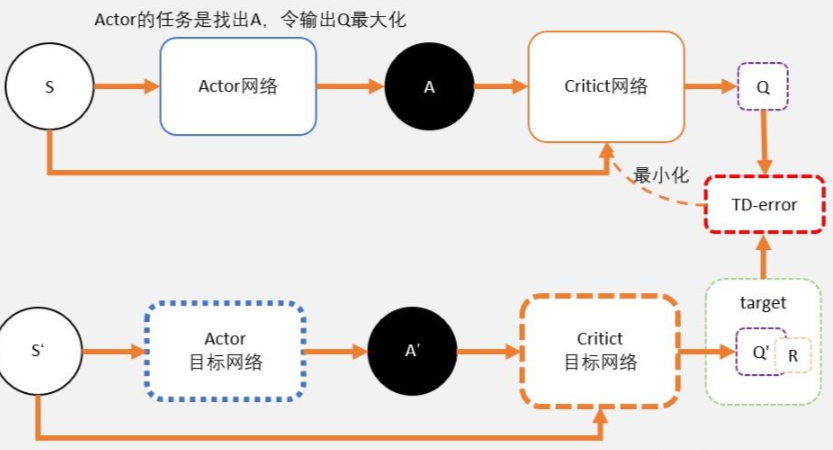
DDPG就是用magic解决DQN不能解决的连续控制型问题。
也就是说,用一个magic函数,直接替代maxQ(s’,a’)的功能。也就是说,我们期待我们输入状态s,magic函数返回我们动作action的取值,这个取值能够让q值最大。这个就是DDPG中的Actor的功能。
我们之前讲DQN也说过,DQN的深度网络,就像用一张布去覆盖Qlearning中的Qtable。这也是DDPG中Critic的功能。
DDPG其实并不是PG,并没有做带权重的梯度更新。而是在梯度上升,在寻找最大值。
Critic
Critic网络的作用是预估Q,虽然它还叫Critic,但和AC中的Critic不一样,这里预估的是Q不是V;
注意Critic的输入有两个:动作和状态,需要一起输入到Critic中;
Critic网络的loss其还是和AC一样,用的是TD-error。
Actor
和AC不同,Actor输出的是一个动作;
Actor的功能是,输出一个动作A,这个动作A输入到Crititc后,能够获得最大的Q值。
所以Actor的更新方式和AC不同,不是用带权重梯度更新,而是用梯度上升。
1、策略梯度法: $ \sum {t’=t}^{T} r(s{i,t’}, a_{i,t’}) - b_i$
2、状态值函数估计轨迹的return: $q(s,a)$
3、优势函数估计轨迹的return:$A(s,a) = q(s,a) - V(s,a)$
4、TD-Error 估计轨迹的return: $r(s,a) + q(s) - q(s’)$
$V^{\pi}(s_t) = \sum^T_{t’=t} r(s_{t’}, a_{t’} )$
training data: ${s_{i,t}, V^{\pi}(s_t) }$
Loss: $ L = 1/2 \sum_i || \hat{V}^{\pi}(s_i) - y_i || ^2$
$$
V(S_t) \larr V(S_t) + \alpha [G_t - V(S_t)]
$$
蒙地卡罗需要完成整个游戏过程,直到最终状态,才能通过回溯计算G值。这使得PG方法的效率被限制。
那我们可不可以更快呢?相信大家已经想到了,那就是改为TD。
但改为TD还有一个问题需要解决,就是:在PG,我们需要计算G值;那么在TD中,我们应该怎样估算每一步的Q值呢?(答案是神经网络)
training data: $ { s_{i,t}, r(s_{i,t}, a_{i,t} ) + \hat{V}^{\pi}{\phi}( s{i, t+1}) }$
引入bias,–> 减少方差variance
Actor: 一个输出策略,负责选择动作;
Critic: 一个负责计算每个动作的分数。
$$
\nabla L_{\theta} = \frac{1}{N} \sum_{i=1}^{N} \sum_{t=0}^{T} \Big[ \nabla_{\theta} log \pi_{\theta}(a_{i,t}|s_{i,t}) \Big(r(s_{i,t}, a_{i,t}) + \gamma \hat{V}{\phi}^{\pi} (s{i,t+1}) - \hat{V}{\phi}^{\pi}(s{i,t}) - b_i \Big) \Big]
$$
lower variance with bias
总结下TD-error的知识:
为了避免正数陷阱,我们希望Actor的更新权重有正有负。因此,我们把Q值减去他们的均值V。有:Q(s,a)-V(s)
为了避免需要预估V值和Q值,我们希望把Q和V统一;由于Q(s,a) = gamma * V(s’) + r - V(s)。所以我们得到TD-error公式: TD-error = gamma * V(s’) + r - V(s)
TD-error就是Actor更新策略时候,带权重更新中的权重值;
现在Critic不再需要预估Q,而是预估V。而根据马可洛夫链所学,我们知道TD-error就是Critic网络需要的loss,也就是说,Critic函数需要最小化TD-error。
PG是一个蒙地卡罗+神经网络的算法。
策略评估
策略提升
VPG更新算法
$$
Policy Graditent: E_{\pi}[\nabla_{\theta}(log_{\pi}(s,a,\theta)) R(\tau)]
$$
$$
Update rule: \Delta \theta = \alpha * \nabla_\theta (
log\pi(s,a,\theta)
) R(\tau)
$$
$\pi : 策略函数,R(): score function 、alpha: lr $
$\nabla L_{\theta} = \frac{1}{N} \sum_{i=1}^{N} \sum_{t=0}^{T} \Big[ \nabla_{\theta} log \pi_{\theta}(a_{i,t}|s_{i,t}) \Big( \sum_{t’=t}^{T} \gamma^{t’-t} r(s_{i,t}, a_{i,t}) - b_i \Big)\Big]$
no bias with higher variance (because use single sample estimate)
PG算法,计算策略梯度的估计器,并将其插入随机梯度上升算法中。最常用的梯度估计器具有以下形式
$$
\hat{g} = \hat{E}t \Big[
\nabla{\theta} log {\pi}_{\theta}(a_t| s_t) \hat{A}_t
\Big] \tag{PPO-1}
$$
E: 表示有限批次样品的经验平均值。
Loss PG:
$$
L^{PG}(\theta) = \hat{E}t \Big[
log {\pi}{\theta} (a_t | s_t ) \hat{A}_t
\Big] \tag{PPO-2}
$$
整条轨迹
$$
\nabla L_{\theta} =
\frac{1}{N} \sum_{i=1}^{N} \sum_{t=0}^{T}
\Big[
\nabla_{\theta} log \pi_{\theta}(a_{i,t}|s_{i,t})
\Big(
\sum_{t’=t}^{T} \gamma^{t’-t} r(s_{i,t}, a_{i,t})
n-step:
$$
\nabla L_{\theta} =
\frac{1}{N} \sum_{i=1}^{N} \sum_{t=0}^{T}
[
\nabla_{\theta} log \pi_{\theta}(a_{i,t}|s_{i,t})
(
\sum_{t’=t}^{t+n} \gamma^{t’-t} r(s_{i,t}, a_{i,t})
trust region / natural policy gradient methods
TRPO 与 PPO 之间的区别在于 TRPO 使用了 KL 散度作为约束条件,虽然损失函数是等价的,但是这种表示形式更难计算,所以较少使用。
约束下最大化更新:
$$
maxmize(\theta) \space \hat{E}t
\Big[
\frac{\pi{\theta}(a_t| s_t) }
{\pi_{\theta_{old}}(a_t | s_t)}
\hat{A}_t
\Big]
\tag{PPO-3,4}
$$
$$
subject \space to \space \hat{E}t
\Big[
KL \big[
\pi{\theta_{old}}(\cdot|s_t),
\pi_{\theta}(\cdot|s_t)
\big]
\Big] \leq \delta
$$
PPO思想1,使用panalty(惩罚)求解无约束优化问题
$$
maximize({\theta}) \space
\hat{E}t \Big[
\frac{\pi{\theta}(a_t| s_t) }
{\pi_{\theta_{old}}(a_t | s_t)}
\hat{A}t - \beta
KL\big[\pi{\theta_{old}} (\cdot| s_t),
\pi_{\theta} (\cdot| s_t)
\big]
\Big] \tag{PPO-5}
$$
single path TRPO;
vine TRPO;
cross-entropy method (CEM)
covariance matrix adaption (CMA) 协方差矩阵自适应
natural gradient, the classic natural policy gradient algorithm
Max KL
RWR
CPI : conservative policy iteration 保守政策迭代 (普通的PG算法)
$$
L^{CPI}(\theta) = \hat{E}t \Big[
\frac{ \pi{\theta}(a_t| s_t) }
{\pi_{\theta_{old}}(a_t| s_t)}
\hat{A}_t
\Big]
= \hat{E}_t [
r_t(\theta) \hat{A}_t
] \tag{6}
$$
PPO_2-CLIP (PPO2思想,对ratio(分布比率)进行clip) 即取一个lower bound,保证梯度更新后效果不会变差
$$
L^{CLIP} (\theta)
= \hat{E}_t \Big[
min\Big(r_t(\theta) \hat{A}_t,
clip \big(r_t(\theta), 1-\epsilon, 1+\epsilon \big) \hat{A}_t \Big)
\Big] \tag{7}
$$
$\epsilon = 0.2$ , $L^{CLIP}$ 是$L^{CPI}$的下界。
PPO_1算法(Adaptive KL Penalty):
$$
L^{KLPEN} (\theta) = \hat{E}t \Big[
\frac{\pi{\theta}(a_t| s_t)}
{\pi_{\theta_{old}}(a_t| s_t)}
\hat{A}t - \beta
KL \big[
\pi{\theta_{old}} (\cdot| s_t),
\pi_{\theta} (\cdot| s_t)
\big]
\Big] \tag{8}
$$
$$
d = \hat{E}t \Big[
KL\big[
\pi{\theta_{old}} (\cdot| s_t),
\pi_{\theta} (\cdot| s_t)
\big]
\Big]
\
if d < d_{targ} / 1.5, \beta = \beta / 2 \
if d < d_{targ} \times 1.5, \beta = \beta \times 2
$$
PPO_2算法(完整目标函数)
$$
L_t^{CLIP+VF+S}(\theta) = \hat{E}_t
\Big[
L_t^{CLIP}(\theta)
- c_1 L_t^{VF}(\theta)
+ c_2 S\pi_{\theta}
\Big]
\tag{9}
$$
S: 表示entropy bonus,当actor和critic共享一套参数时,需要加的误差项 S :an entropy bonus,在exploration时很有用
$L_t^{VF}$ squared-error loss $(V_{\theta(S_t)} - V_t^{targ})^2$
PG Advantage Estimator:
$$
\hat{A}t = -V(s_t) + r_t + \gamma r{t+1} + …
+ \gamma^{T-t+1} r_{T-1}
+ \gamma^{T-t} V(s_T)
\tag{10}
$$
GAE也是用于平衡bias和variance的一种方法,公式比较复杂一点,思想是$TD(\lambda)$
truncated version of generalized advantage estimator(GAE):
$$
\hat{A}t = \delta_t + (\gamma \lambda )\delta{t+1} + … + … +
(\gamma \lambda )^{T-t+1 }\delta_{T-1} \tag{11,12} \
where \space \gamma_t = r_t + \lambda V(s_{t+1}) - V(s_t)
$$
No clipping or penalty:
$$
L_t(\theta) = r_t(\theta)\hat{A}_t
$$
Clipping:
$$
L_t(\theta) = min \Big(
r_t(\theta)\hat{A}_t,
clip\big(r_t(\theta), 1-\epsilon, 1+\epsilon\big)\hat{A}_t
\Big)
$$
KL penalty (fixed or adaptive)
$$
L_t(\theta) = r_t(\theta)\hat{A}t -
\beta KL
\big[
\pi{\theta_{old}}, \pi_{\theta}
\big]
$$
Robot
路径规划
A*
Dijkstra,
D*
TEB
2
3
运动恢复结构 从多张图像或视频序列中自动地恢复出相机的参数以及场景三维结构的技术
鸟瞰视角(Bird’s Eye View,简称BEV)是一种从上方观看对象或场景的视角,就像鸟在空中俯视地面一样。在自动驾驶和机器人领域,通过传感器(如LiDAR和摄像头)获取的数据通常会被转换成BEV表示,以便更好地进行物体检测、路径规划等任务。BEV能够将复杂的三维环境简化为二维图像,这对于在实时系统中进行高效的计算尤其重要。
BEV(鸟瞰视图)景物表示方法
给定来自多个车载摄像机图像获得校正的360度BEV图像。校正的BEV图像被分割成语义类别,并且包括对遮挡区域的预测。
神经网络方法并不依赖手动标记数据,而是在模拟合成数据集上进行训练,并泛化到现实世界数据。以语义分割图像作为输入,可以减少模拟数据与现实世界数据之间的现实差距,并也证明该方法可以成功应用于现实世界中。
单应性变换应用于车载摄像头的四个语义分割图像,将其转换为BEV;IPM直接用homography转换误差很大(路面平坦的假设),而这种方法在无视觉失真情况下学习如何计算准确的BEV图像。
一是单输入模型,基于DeepLabv3+,其中主干分别采用MobileNetV2 和 Xception测试;二是 多输入模型,基于U-Net,做了一些变型。
FISHING Net体系结构如图所示:多个神经网络,每个传感器模态(雷达,雷达和摄像头)一个,接收一系列输入传感器数据,并输出代表3个目标类别(弱势道路用户即VRU、车辆和背景)的一系列自上而下的共享语义网格;然后,使用聚合函数融合序列,以输出语义网格的融合序列。
本文提出BEV-Seg,做BEV语义分割,这项任务可根据侧视(不是鸟瞰)摄像头的RGB图像预测BEV的像素级语义分割。存在两个主要挑战:从侧视图到鸟瞰图的视图转换,以及学习迁移到未见过的领域。作者提出的两级感知流水线方法,可显式预测像素深度,并以有效的方式将其与像素语义相结合,使模型利用深度信息来推断BEV中目标的空间位置。其中迁移学习的实现是,抽象高级几何特征,并预测跨不同领域通用的中间表示(IR)。
BEV-Seg流水线如图所示:
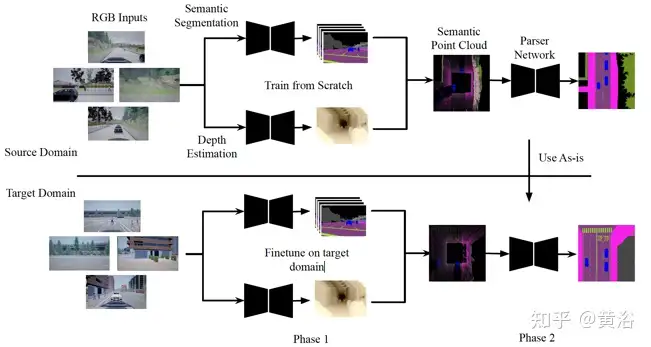
第一步,N个RGB道路场景图像由不同角度的摄像头捕获,并分别通过语义分割网络S和深度估计网络D;所得到的侧视语义分割和深度图被组合并投影到3-D变成语义点云;这里点云语义图是不完整的。第二步,然后将该点云投影到不完整的鸟瞰图中,再将其输入到一个parser network预测最终的鸟瞰图分割,做“填洞”和“平滑”等工作。
补充一些细节:对于侧视语义分割,用HRNet主干,这也是用于语义分割的最新卷积网络。对于单目深度估计,用与骨干网相同的HRNet来实现SORD模型。对于这两个任务,在所有四个视图训练相同的模型。生成的语义点云沿着垂直高度方向投影到512x512图像上。训练一个单独的HRNet模型作为parser network,进行最终的鸟瞰语义分割。
通过模块化和抽象性做到的迁移学习包括:
实验结果比较如下:VPN做比较

BEVFormer、LSS、BEVDET
https://zhuanlan.zhihu.com/p/365561705
9 Lift, Splat, Shoot: Encoding Images from Arbitrary Camera Rigs by Implicitly Unprojecting to 3D,arXiv 2008.05711
10 Understanding Bird’s-Eye View Semantic HD-maps Using an Onboard Monocular Camera,arXiv 2012.03040
BEV感知理论与实践 - 深蓝学院 - 专注人工智能与自动驾驶的学习平台

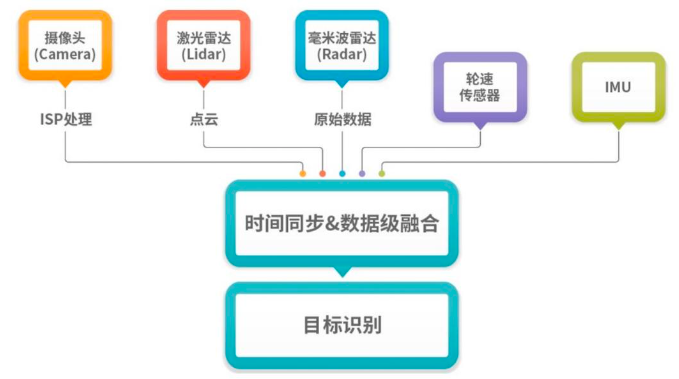
前融合
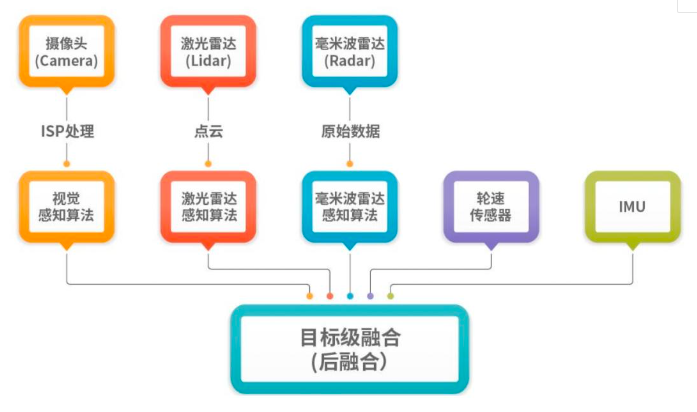
后融合
DeepSpeed是微软推出的大规模模型分布式训练的工具,主要实现了ZeRO并行训练算法。
本文是huggingface的DeepSpeed文档的笔记,做查询和备忘,初次学习建议结合原始文档食用。原始文档链接:
https://huggingface.co/docs/transformers/main/main_classes/deepspeed
目前主流的大模型分布式训练主要包括两种:
数据并行训练
模型并行训练
RL可以使用的虚拟化环境(仿真器)
学生邮箱,免费一年
MuJoCo是目前机器人强化学习中最流行的仿真器。它提供了很多有趣复杂的环境,通常以连续动作环境为主。所以,但我们想在这样的环境中测试自己算法的性能的时候,就必须下载Mujoco并且需要有密钥才可以使用它。
Player和edu版本可免费使用,pro版需要购买。
Vrep是一款动力学仿真软件,主要定位于机器人仿真建模领域,可以利用内嵌脚本、ROS节点、远程API客户端等实现分布式的控制结构,是非常理想的机器人仿真建模的工具。
https://zhuanlan.zhihu.com/p/32967121

https://zhuanlan.zhihu.com/p/367660310
Isaac SDK(软件开发工具包):Isaac SDK 提供了一组用于构建机器人应用的库和工具。它包含了丰富的功能模块,如感知、规划、控制和通信等,帮助开发人员快速构建强大的机器人应用程序。
Isaac Sim(仿真环境):Isaac Sim 是 NVIDIA Isaac 平台的仿真环境,用于验证和调试机器人应用。它基于虚幻引擎,提供了逼真的物理模拟和可视化工具,帮助开发人员在真实环境之前进行快速迭代和测试。
Isaac Robot Engine(机器人引擎):Isaac Robot Engine 是 NVIDIA Isaac 平台的核心组件之一,用于实时控制机器人硬件。它提供了低延迟和高性能的机器人控制能力,支持各种传感器和执行器的集成。
Isaac Apps(应用程序):Isaac Apps 是一组预构建的机器人应用程序,用于演示和启发开发人员。它们涵盖了各种典